Geometria Plana – Polígonos

POLÍGONOS

Veja um exemplo de polígono:

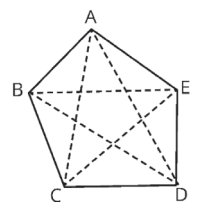
Os pontos A, B, C, D e E são chamados de vértices.

Num polígono, os segmentos que unem dois vértices consecutivos são chamados de lados.

No polígono apresentado na figura, os lados são: AB, BC, CD, DE e AE.

As diagonais são os segmentos que unem dois vértices não consecutivos.

CONVEXIDADE DO POLÍGONO

POLÍGONO CONVEXO

É quando, dados dois pontos quaisquer do polígono, o segmento de reta que o une esses dois pontos está inteiramente contido no polígono.

POLÍGONO CÔNCAVO

Um polígono é dito côncavo quando é possível escolher dois pontos do polígono, de modo que o segmento de reta que une esses pontos não está inteiramente contido no polígono.

GÊNERO DO POLÍGONO

Um polígono com n lados possui n vértices. O número de lados nos fornece o gênero do polígono. O nome do polígono depende do número de lados. Como a seguir:

3 lados → Triângulo

4 lados → Quadrilátero

5 lados → Pentágono

6 lados → Hexágono

7 lados → Heptágono

8 lados → Octógono

9 lados → Eneágono

10 lados → Decágono

11 lados → Undecágono

12 lados → Dodecágono

13 lados → Tridecágono

14 lados → Tetradecágono

15 lados → Pentadecágono

16 lados → Hexadecágono

17 lados → Heptadecágono

18 lados → Octadecágono

19 lados → Eneadecágono

20 lados → Icoságono

OBSERVAÇÃO

Curiosidade

Googólgono é um polígono com um googol de lados. Se regular, para todos os efeitos (devido ao seu ângulo de praticamente 180º), tal figura seria praticamente igual a um círculo. Se os lados de um googólgono regular tivessem o mesmo comprimento do raio de um próton (aproximadamente 0,8 x 10^-15 m, ou 0,8 femtometros), o raio do polígono seria de aprox. 1,27 x 10⁸⁴ m, e sua área de 5,09 x 10¹⁶⁸ m².

Para se ter uma ideia da ordem de grandeza desta figura, o diâmetro do Sol é de “apenas” 1,39 x 10⁹ m, ou 1,39 gigametros, e o comprimento estimado do universo visível (distância percorrida pela luz desde o Big Bang) é de 1,37 x 10²⁶ m, ou 13,7 bilhões de anos-luz. Em relação à área, o disco da Via Láctea tem uma superfície de cerca de 7 x 10⁴¹ m².

_{Fonte: Wikipédia, a enciclopédia livre.}

*O googol (lê-se gugol – sua forma de escrita em Portugal) é o número 10¹⁰⁰, ou seja, o dígito 1 seguido de cem zeros.

NÚMERO DE DIAGONAIS DE UM POLÍGONO

O número e diagonais de um polígono é dado pela fórmula:

Vale ressaltar que o triangulo não possui diagonais mas em todo polígono com quatro ou mais lados é possível calcular a quantidade de diagonais do polígono levando em conta apenas o seu número de lados.

Para isso vamos observar que num polígono a quantidade de diagonais que parte de qualquer um de seus vértices é sempre a mesma.

Observe o pentágono abaixo:

Não importa o vértice que você escolha, sempre partirá dele duas diagonais. Isso ocorre com qualquer polígono! Num polígono com n lados quantas diagonais partem de cada vértice?

Você consegue explicar o motivo dessa relação?

Uma diagonal é o segmento que une dois vértices não consecutivos. Por isso, se temos n vértices formamos n – 3 diagonais pois esse vértice não pode ser ligado ao seus vértices consecutivos (um de cada lado) e nem nele próprio.

Dessa forma, fica bastante simples obtermos uma fórmula para o cálculo do total de diagonais de um polígono.

Como o número de vértices é igual ao número de lados do polígono, segue que teremos, com extremidade nos n vértices:

Mas isso não nos dá ainda a fórmula que estamos procurando pois como sabemos que uma diagonal tem extremidades em dois vértices estamos então contando duas vezes cada diagonal. Para resolvermos esse problema basta dividirmos por dois a fórmula anterior:

SOMA DOS ÂNGULOS INTERNOS DE UM POLÍGONO

A soma dos ângulos internos de um polígono, medida em graus, é dada pela fórmula:

Demonstração:

De forma geral, um polígono convexo, pode ser decomposto em triângulos, se traçarmos as diagonais a partir de qualquer um de seus vértices:

Observe a figura abaixo:

Note que existe uma relação entre a quantidade de lados do polígono e a quantidade de triângulos que podem formar. Veja a tabela abaixo:

Observe que a soma dos ângulos internos do polígono é a soma dos ângulos internos de todos os triângulos obtidos na decomposição proposta.

Dessa forma, temos que a soma dos ângulos internos do polígono pode ser obtida por .

OBSERVAÇÃO

Cada vértice de um polígono convexo possui um ângulo interno (aⁱ) e um ângulo externo (aᵉ), que são suplementares, isto é, aⁱ + aᵉ = 180

SOMA DOS ÂNGULOS EXTERNOS DE UM POLÍGONO

A soma dos ângulos externos de qualquer polígono é sempre 360°, independente do número de lados do polígono.

Sᵉ = 360°

Demonstração:

Observe inicialmente o triângulo. Note que em cada vértice a soma do ângulo interno e do ângulo externo gera um ângulo raso (180°).

Dessa forma, para obtermos a soma dos ângulos externos podemos escrever as seguintes equações:

Somando, membro a membro, obtemos:

Sabemos que portanto .

Será que isso vale para todos os polígonos?

Queremos mostrar que sim!

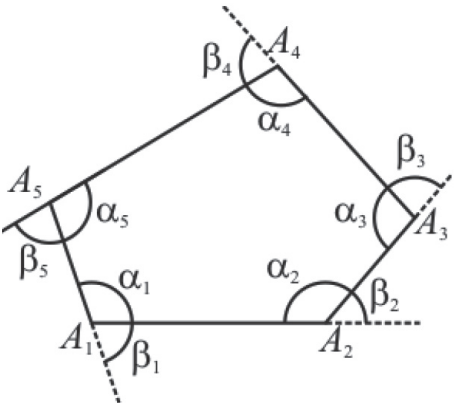
E para isso, utilizaremos a mesma ideia exposta acima. Escreveremos as equações para todos os vértices de um polígono de n lados:

…

Somando, membro a membro, obtemos:

Sabemos que a soma dos ângulos internos de um polígono é dada por:

Substituindo na equação, temos:

POLÍGONO EQUIÂNGULO

Um polígono é chamado de equiângulo, quando possui todos os ângulos internos congruentes entre si. Dessa forma, todos seus ângulos externos também serão congruentes entre si.

MEDIDA DE CADA ÃNGULO INTERNO DO POLÍGONO EQUIÂNGULO

Acabamos de ver que o polígono equiângulo possui todos os ângulos internos congruentes entre si, isto é, com a mesma medida. Logo a medida de cada ângulo interno será a soma de todos os ângulos internos, divido pelo número de ângulos internos. Então, .

Como , segue que a medida de cada ângulo interno é dada por 

MEDIDA DE CADA ÂNGULO EXTERNO DO POLÍGONO EQUIÂNGULO

Vimos que o polígono equiângulo, além de possuir todos ângulos internos congruentes entre si, também possui todos seus ângulos externos congruentes entre si. Usando o mesmo raciocínio, temos que a medida de cada ângulo externo será .

Como podemos escrever que a medida de cada ângulo externo é dada por:

POLÍGONO EQUILÁTERO

Um polígono é chamado de equilátero quando possui todos os lados congruentes entre si.

POLÍGONO REGULAR

Quando o polígono for equiângulo e equilátero ao mesmo tempo.

Polígono regular

Observações:

Note que o polígono regular é equiângulo, logo possui todos os ângulos internos congruentes entre si, e todos ângulos externos congruentes entre si. Dessa forma, no polígono regular também podemos dizer que:

 e 

Além disso, quando já se conhece a medida de um desses dois, para calculara medida do outro, basta lembrar que juntos eles representam meia-volta, isto é   

Todo polígono regular é inscritível em uma circunferência.

Todo polígono regular é circunscritível em uma circunferência.

DIAGONAIS QUE PASSAM PELO CENTRO DE UM POLÍGONO REGULAR

O número de diagonais (dᶜ) que passem pelo centro de um polígono regular depende do número de lados, e é dado por:

dᶜ = { 0, quando n é ímpar

    =  { n/2 , quando n é par 

Isto é, quando o polígono regular tem um número ímpar de lados, o número de diagonais que passam pelo seu centro é zero, ou seja, não existem diagonais passando pelo centro. Exemplos de polígonos regulares com número ímpar de lados: triângulo equilátero, pentágono regular, heptágono regular etc.

Quando o número de lados é par, o número de diagonais que passam pelo centro do polígono regular é a metade do número de lados. Dessa forma, por exemplo, no quadrado o número de lados é 4, então o número de diagonais que passam pelo seu centro é 2. No hexágono regular o número de lados é 6, então o número de diagonais que passam pelo seu centro é 3.

Exemplos:

01. Em um hexágono regular:

a) Quantas diagonais partem de cada vértice?
b) Qual o total de diagonais?
c) Quanto vale a soma dos ângulos internos?
d) Quanto vale a soma dos ângulos externos?
e) Quanto vale a medida de cada ângulo interno?
f) Quanto vale a medida de cada ângulo externo?
g) Quantas diagonais passam pelo seu centro?

Resolução:

a) Quantas diagonais partem de cada vértice?

O número de diagonais que partem de cada vértice de um polígono convexo é dada por n – 3, pois devemos desconsiderar os vértices consecutivos e o próprio vértice, dessa forma, no hexágono de cada vértice partem 3 diagonais.

b) Qual o total de diagonais?

O total de diagonais é obtido a partir da seguinte fórmula:

d = n . (n-3)/2 

Como no hexágono n = 6 é fácil ver que

d = 6 . (6-3)/2 = 6 . (3)/2 = 18/2 = 9

c) Quanto vale a soma dos ângulos internos?

A soma dos ângulos internos pode ser obtida a partir da fórmula Si = (n – 2) ·180°.

Como no hexágono n = 6, temos que Si =(6 – 2) ·180° =(4) ·180° = 720°

d) Quanto vale a soma dos ângulos externos?
A soma dos ângulos externos sempre vale 360º.

e) Quanto vale a medida de cada ângulo interno?

Para obter a medida de cada ângulo interno basta dividir a soma dos ângulos internos por seis, visto que o hexágono
possui seis ângulos internos e são todos congruentes.

Dessa forma, temos que aⁱ = 720°/6 = 120°.

f) Quanto vale a medida de cada ângulo externo?

Para obter a medida de cada ângulo externo basta dividir a soma dos ângulos externos por seis, visto que o hexágono
possui seis ângulos externos e são todos congruentes.

Dessa forma, temos que aᵉ = 360°/6 = 60° 

Um outro caminho é perceber que o ângulo interno e o externo são suplementares.

g) Quantas diagonais passam pelo seu centro?

A quantidade de diagonais que passa pelo centro de um polígono regular é 

dada por dᶜ = { 0, quando n é ímpar

                     =  { n/2 , quando n é par 

No caso do hexágono, temos que n = 6, portanto dᶜ = 6/2 = 3 

02. O hexágono ABCDEF da figura é regular.

Calcule a medida do ângulo α assinalado.

Resolução:

Sabemos que AB = BC  e que o ângulo ABC = 120° . Dessa forma, é fácil perceber que os ângulos BÂC e BCA medem 30°.

Como os triângulos ∆ABC e ∆CDE são congruentes, sabemos que ECD = 30°.

Portanto, como ângulo BCD = BCA + ACE + ECD  temos que 120° = 30° + ACE + 30° → ACE = 60°.

03. A,B,C,D e E são, nessa ordem, vértices consecutivos de um pentágono regular ABCDE as diagonais AC e BD cortam-se em P.

Calcule a medida do ângulo CPD .

Resolução:

Como temos um pentágono regular podemos determinar os ângulos BDC e ACD facilmente, pois sabemos que cada ângulo interno do pentágono vale 108°

Observe que o triângulo ∆ABC é isósceles como B = 108° temos que ACB = 36° daí concluímos que ACD = 72° 

De forma análoga ao caso anterior temos que o triângulo ∆BDC é isósceles e o ângulo BDC = 36°.

Observe a figura abaixo:

Queremos calcular o ângulo CPD e como já sabemos que PDC= 36º e PCD = 72º podemos concluir que CPD = 72º pois a soma dos ângulos internos de um triângulo vale 180°.

04. A,B,C,D,E,F,G,H,I e J são, nessa ordem, vértices consecutivos de um decágono regular. Calcule a medida do menor ângulo formado pela mediatriz de AB com a bissetriz externa de B^ .

Resolução:

Observe parte do decágono regular representado abaixo:

Sabemos que os ângulos internos medem 144º e os externo 36º. Dessa forma, após o esboço, percebe-se que o ângulo que  procuramos é o ângulo BKM. Note que o ângulo KBM = 18° pois é obtido a partir da bissetriz do ângulo externo de B e, o ângulo KMB = 90° pois é formado pela mediatriz de AB .

Assim concluímos que o ângulo que procuramos vale 72º pois a soma dos ângulos internos de um triângulo vale 180º.